Никто конкретики не вносит, все знают как должно быть,
но как будет на самом деле-никто не ручается.
Энергетический парадокс самоиндукции,
через эксперимент к новой физической модели.
Опубликовано: 22/11/25
Современная физика сталкивается с системным методологическим кризисом в описании широкого класса явлений, представляющих собой отклик системы на внешнее воздействие, направленный на компенсацию этого воздействия и перераспределение энергии. К этим явлениям, определяющим энергообмен в физических системах и формирующим, по сути, каркас реальности, относятся трение, инерция, самоиндукция, кипение, упругость и другие. Глубинная, единая физическая природа этих сил, а также принципы управления сопряженной с ними энергией остаются нераскрытыми. Преодоление этого феноменологического барьера является необходимым условием для снятия фундаментальных ограничений, сдерживающих разработку технологий, основанных на иных физических принципах.
Явление самоиндукции является частным случаем проявления универсального принципа Ле Шателье – Брауна в электродинамике. Согласно этому принципу, система, находящаяся в равновесии, противодействует любому внешнему воздействию, стремясь компенсировать производимое изменение.
Применительно к электрической цепи таким воздействием служит изменение силы тока, выводящее систему из равновесия. В качестве ответной реакции цепи на это воздействие возникает электродвижущая сила самоиндукции. Её фундаментальное свойство, установленное экспериментально (правило Ленца), заключается в том, что она всегда направлена таким образом, чтобы противодействовать изменению исходного тока.
Таким образом, ключевая роль ЭДС самоиндукции заключается в организации противодействия внешнему возмущению (изменению тока), что и составляет её суть «внутренней реакции» системы.
В контексте принципа Ле Шателье-Брауна и явления самоиндукции, под системой понимается мысленно выделенная из окружающего мира совокупность взаимодействующих элементов, образующих целостное образование с собственным, внутренним состоянием.
Разграничение понятий энергии магнитного
поля и ЭДС самоиндукции.
Опубликовано: 23/11/25
При классическом рассмотрении цепи с индуктивностью возникновение ЭДС самоиндукции объясняют наличием магнитного поля, а накопленную в этом поле энергию связывают с работой по созданию ЭДС самоиндукции. Подобное описание смешивает (отождествляет) сущности разной физической природы: причину (изменение тока, порождающее поле), следствие (ЭДС как реакцию на это изменение) и меру запаса (энергию как интегральный итог процесса). Эта методологическая неточность затрудняет фундаментальное понимание переходных процессов, служит источником парадоксов в учебных интерпретациях и препятствует адекватному описанию явления.
Энергия магнитного поля: мера накопленного потенциала (функция состояния).
Энергия W, локализованная в магнитном поле контура с индуктивностью L, является функцией состояния системы. Это означает, что её значение в любой момент времени t однозначно определяется текущим состоянием системы, характеризуемым мгновенной силой тока I(t):
W = (L * I²) / 2 (1)
где I — мгновенное значение силы тока.
Ключевые свойства W как функции состояния:
- Определяется только текущим состоянием: Величина W(t) зависит исключительно от значения I(t) в момент t и не зависит от того, каким образом это значение было достигнуто.
- Инвариантность к истории процесса: Одинаковый ток (и, следовательно, одинаковая энергия) могут быть получены как в результате быстрого, так и бесконечно медленного (квазистатического) процесса. Энергия — это итог, а не описание пути.
Таким образом, энергия W представляет собой меру накопленного потенциала — статическую характеристику системы, фиксирующую результат завершённого энергообмена. Если провести механическую аналогию, W — это потенциальная энергия деформированной пружины, а не сила, которую она создаёт в процессе деформации.
ЭДС самоиндукции: мера мгновенного динамического ответа.
В противоположность энергии, Электродвижущая сила самоиндукции E_s является функцией процесса. Она не характеризует состояние системы, а описывает её динамический отклик на изменение этого состояния. E_s существует исключительно в переходных (нестационарных) режимах и количественно определяет скорость процесса:
Es = -L * (dI / dt) (2)
Её определяющие особенности:
- Существует только при изменении тока (dI/dt ≠ 0): В установившемся режиме E_s тождественно равна нулю, независимо от величины запасённой энергии W.
- Зависит от скорости процесса: Её величина определяется не значением тока, а скоростью его изменения.
Эта величина характеризует мгновенную интенсивность противодействия контура изменению тока. Она выступает мерой мощности реакции системы на возмущение, а не мерой накопленного в ней потенциала. Продолжая механическую аналогию, E_s — это сила упругости, возникающая в пружине в процессе её сжатия или растяжения и пропорциональная скорости этой деформации. Это динамическое ощущение, процесс. ЭДС самоиндукции существует только в момент, когда вы меняете степень сжатия пружины (открываете или закрываете дверь).
ЭДС самоиндукции (E_s) и энергия магнитного поля (W) являются физически разными величинами, их независимость доказывается двумя мысленными экспериментами:
- Ситуация А: Соленоид с большой индуктивностью L, маленьким током I₁. W₁ = L*I₁²/2.
- Ситуация Б: Проводник (например, шина) с малой индуктивностью L/1000, но большим током I₂ = √1000 * I₁ ≈ 31.6 * I₁. W₂ = (L/1000) * (1000*I₁²)/2 = L*I₁²/2 = W₁.
Энергия одинакова. Но при одинаковой скорости изменения тока dI/dt в ситуации Б ЭДС самоиндукции будет в 1000 раз меньше, чем в ситуации А (E_s = - (L/1000) * dI/dt). При фиксированной энергии W: Система с малой L и большим I может иметь колоссальную E_s при резком изменении тока (dI/dt), в то время как система с большой L и малым I, хранящая ту же энергию W, будет иметь малую E_s при той же скорости изменения тока. ЭДС определяется не энергией, а комбинацией L и dI/dt.
Поставить между энергией магнитного поля и эдс самоиндукции знак равенства — всё равно что сказать: "Расстояние от Москвы до Владивостора (итог, аналог энергии) равно скорости поезда (процесс, аналог ЭДС)". Это абсурдно. Кроме того, одинаковое расстояние можно проехать на поезде или долететь на самолёте. Итог один, расстояние одинаково, а "сила" процесса перемещения — разная.
Превышение работы ЭДС самоиндукции над
затратами источника питания.
Опубликовано: 21/12/25
Аннотация.
В работе представлены результаты экспериментального исследования переходного процесса при коммутации тока в последовательной RL-цепи. Высокоточный временно́й анализ осциллограмм выявил аномалию во временно́й корреляции между моментом прекращения изменения тока и формированием импульса ЭДС самоиндукции. Напряжение на катушке индуктивности в виде мощного импульса возникает после завершения фронта запирания ключевого транзистора, то есть в момент, когда производная тока dI/dt через индуктивность теоретически должна быть равна нулю. Сопоставление экспериментальных данных с расчётами по классической формуле Eₛ = –L (dI/dt) выявляет физическую несовместимость наблюдаемого процесса с классической моделью по временны́м параметрам.
Фундаментальное соотношение Eₛ = –L (dI/dt), описывающее явление самоиндукции, постулирует прямую и мгновенную причинно-следственную связь: изменение тока через индуктивный элемент является непосредственной причиной возникновения электродвижущей силы. Целью настоящей работы является экспериментальная проверка временно́й корреляции между изменением тока и генерацией ЭДС самоиндукции в момент размыкания последовательной RL-цепи.
Методика эксперимента.
Исследование проведено на последовательной RL-цепи, содержащей источник постоянного напряжения 12 В, катушку индуктивности с воздушным сердечником (L = 58.31 мкГн) и ключевой элемент на полевом транзисторе RSM1701K0W. Управляющие импульсы на затвор транзистора подавались с внешнего генератора UTG962E через специализированный драйвер TC4452. Амплитуда управляющего напряжения +15 В гарантировала режим глубокого насыщения транзистора до коммутации.
Регистрация сигналов осуществлялась цифровым осциллографом Siglent SDS1204X-E (200 МГц, 1 Гвыб/с) по двум каналам:
- Канал 1 (жёлтый луч): Напряжение на затворе транзистора U_gs(t).
- Канал 2 (бордовый луч): Напряжение на катушке индуктивности U_L(t), регистрируемое как ЭДС самоиндукции Eₛ(t).
Временной анализ осциллограмм.
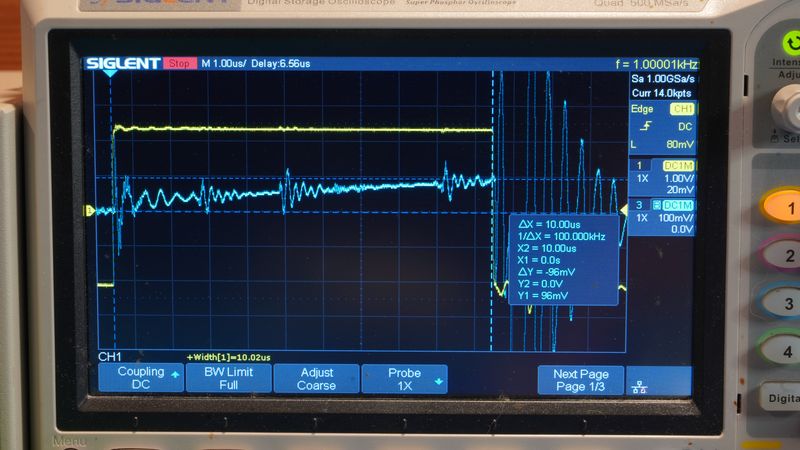
Детальный анализ осциллограмм с использованием временны́х маркеров позволил установить следующую последовательность событий:
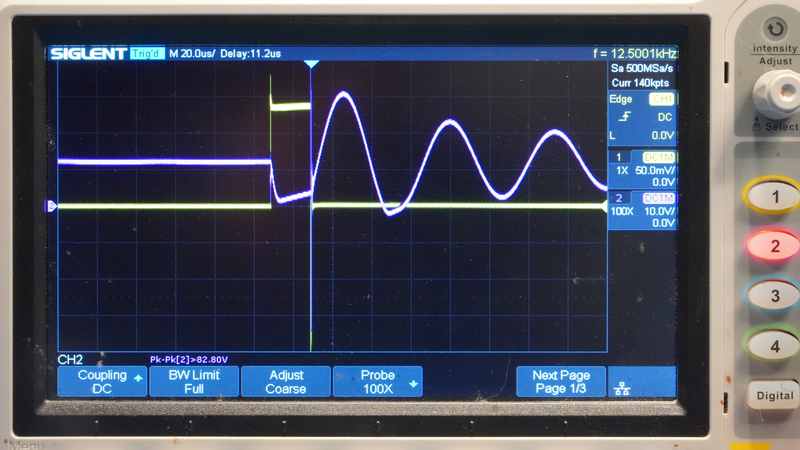
- Напряжение на затворе транзистора (жёлтый луч) достигает нулевого уровня. Этот момент (t₀) маркирует завершение процесса перехода ключа из открытого в закрытое состояние и, соответственно, прекращение изменения тока в силовой цепи. К моменту t₀ цепь разомкнута.
- В момент t₀ и далее на осциллограмме фиксируется начало формирования импульса ЭДС самоиндукции (бордовый луч) амплитудой до 1540 В.
Наблюдаемый на канале 1 отрицательный выброс после основного фронта является индустрированной
помехой (ёмкостной/индуктивной наводкой) от мощного уже сформировавшегося импульса ЭДС
самоиндукции (бордовый луч) на цепь управления и не рассматривается как часть управляющего
сигнала.
Обсуждение результатов.
- Установлен факт нарушения причинной последовательности. Экспериментально зафиксировано, что импульс ЭДС самоиндукции начинает формироваться после полного закрытия транзистора, то есть в момент, когда ток в цепи и его изменение (di/dt) прекратились. Это противоречит исходному постулату закона E = –L di/dt, требующему синхронности ЭДС и изменения тока.
- Классическая формула самоиндукции неадекватна. Поскольку генерация ЭДС происходит в отсутствие изменения тока через ключевой элемент, прямое применение соотношения E = –L di/dt для описания процесса возникновения ЭДС в момент коммутации физически некорректно.
- Нарушен фундаментальный принцип, вытекающий из закона электромагнитной индукции Фарадея в применении к самоиндукции: ЭДС самоиндукции существует тогда и только тогда, когда изменяется сила тока в контуре (dI/dt ≠ 0). Эксперимент демонстрирует, что мощный импульс ЭДС формируется после завершения изменения тока (dI/dt → 0), то есть в условиях, когда, согласно классической формуле, она должна быть равна нулю.
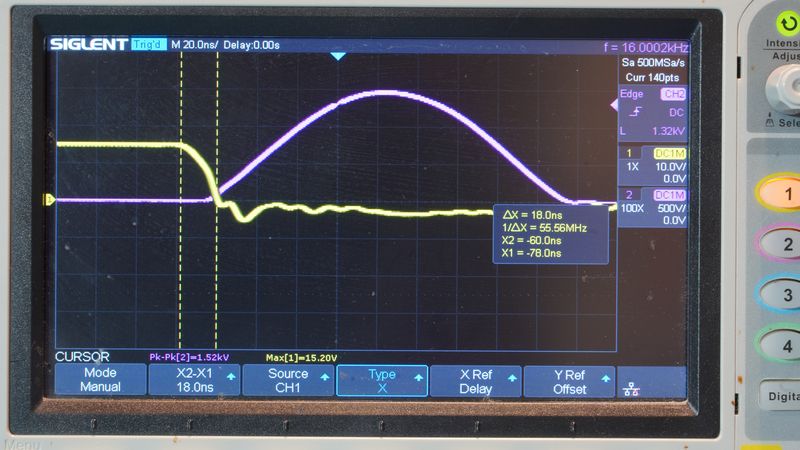
Более детальная осциллограмма предоставляет доказательство, позволяющее однозначно
разделить во времени процесс коммутации (жёлтый луч, затвор транзистора) и процесс
генерации ЭДС (бордовый луч, сток/исток транзистора).
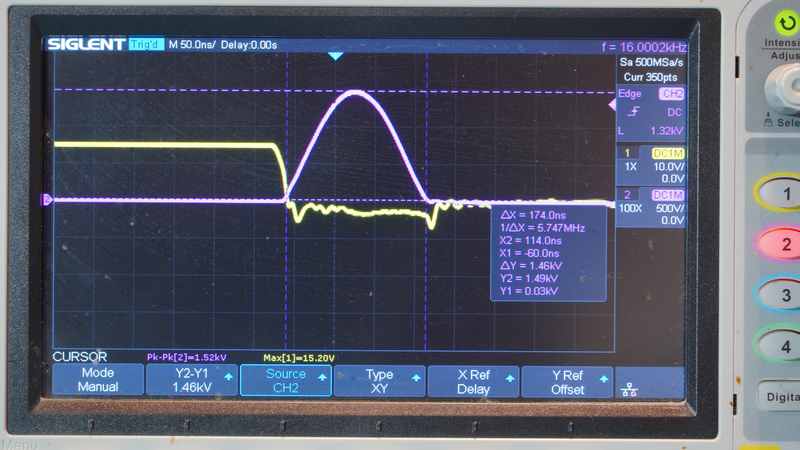
На осциллограмме фиксируется фронт сигнала на затворе транзистора (жёлтый луч), соответствующий срезу управляющего напряжения от уровня насыщения (+15 В) до нуля. Длительность этого переходного процесса, определяемая по установлению устойчивого низкого уровня на затворе, составляет τ_комм ≈ 18 нс. Критически важно, что на протяжении всего этого интервала, когда скорость изменения тока через ключевой элемент (dI/dt) теоретически максимальна, значимого роста напряжения ЭДС самоиндукции на катушке (канал 2, бордовый луч) не наблюдается. Критически важно, что на протяжении всего этого интервала, когда скорость изменения тока через ключевой элемент (dI/dt) теоретически максимальна, при этом рост напряжения ЭДС самоиндукции на катушке (бордовый луч) не наблюдается.
Резкий рост напряжения ЭДС начинается строго после момента t₀, когда переходный процесс на затворе завершён и транзистор переходит в полностью закрытое состояние. Амплитуда генерируемого импульса достигает значения E_peak ≈ 1.5 кВ. Длительность основного импульса, измеренная от начала нарастания до момента заметного спада амплитуды, составляет τ_имп ≈ 174 нс.
Данная осциллограмма визуализирует ключевой временной парадокс, который не может быть объяснён в рамках классической модели, описываемой соотношением E = –L (dI/dt):
Вывод.
- Экспериментально установлено, что момент формирования импульса ЭДС самоиндукции начинается после прекращения изменения тока в цепи, то есть после закрытия транзистора. Это свидетельствует о том, что классическое соотношение E = –L (dI/dt) не является достаточным для описания механизма генерации ЭДС в момент ультрабыстрой коммутации.
- Классическая модель трактует ЭДС самоиндукции как силу противодействия, возникающую непосредственно в момент и вследствие изменения тока. Наблюдаемый процесс указывает на иную природу явления: ЭДС самоиндукции ведёт себя как автономный энергетический отклик системы. Этот отклик инициируется изменением тока (коммутацией), но развивается по собственным законам с характерным временем развития и релаксации (τ_имп ≈ 174 нс), существенно превышающим длительность триггерного события (τ_комм ≈ 18 нс).
- Таким образом, результаты указывают на необходимость выхода за рамки квазистатической модели с сосредоточенными параметрами. Для адекватного описания требуется рассмотрение системы как распределённой электродинамической структуры, в которой переходный процесс является не локальным откликом на dI/dt, а объёмным образованием энергии с конечным временем установления.
- Согласно классической модели: Максимум ЭДС самоиндукции должен совпадать по времени с максимумом скорости изменения тока (dI/dt), то есть наблюдаться в интервале активной коммутации длительностью τ_комм ≈ 18 нс.
- Согласно экспериментальным данным: Активная генерация ЭДС является отдельным, последующим событием. Её начало отсчитывается от момента завершения коммутации (t₀), а её длительность τ_имп ≈ 174 нс на порядок превышает длительность самого коммутационного события.
Выключение транзистора в нашей схеме — это не причина энерговыделения, а лишь триггер. Это подобно хлопку в горах, вызывающему лавину.
«Бухгалтерия по Ломоносову» (классическая модель закона сохранения) занята лишь тем, что взвешивает снег до и после обвала. Она констатирует: масса снега на склоне уменьшилась, масса у подножия — увеличилась. Энергия хлопка пренебрежимо мала, интегральный баланс масс сходится. С её точки зрения всё объяснимо, а лавина как таковая не представляет интереса — это всего лишь «перераспределение снега». Теорема Нётер, связывающая законы сохранения с симметриями системы, лишь объясняет, почему и при каких идеальных условиях «Бухгалтерия по Ломоносову» возможна и работает.
Однако глупо ограничиваться лишь «взвешиванием снега» (подсчётом интегральных энергий до и после). Истинная задача исследователя и инженера — понять механизм лавины и научиться использовать её колоссальную, хотя и кратковременную, энергию.
Мой эксперимент — это попытка не просто признать «факт обвала», а зафиксировать и измерить параметры самой лавины: её пиковую мощность, скорость распространения фронта, колебательный спектр. Только так можно совершить переход от констатации баланса к созданию технологий, преобразующих разрушительный импульс поля в полезную работу. Это и есть сдвиг парадигмы: от физики равновесных состояний — к физике и инженерии мощных нестационарных событий.
Экспериментальное доказательство ошибочности
постулата классической самоиндукции.
Опубликовано: 09/12/25
Классическая теория самоиндукции основывается на фундаментальном принципе, вытекающем из закона электромагнитной индукции Фарадея: ЭДС самоиндукции возникает ровно в те моменты и существует ровно столько времени, пока происходит изменение тока (di/dt ≠ 0).
Количественное выражение этого принципа — формула ε_s = –L (dI/dt) — устанавливает жёсткую синхронность (мгновенность) между причиной (изменение тока) и следствием (возникновение ЭДС). Данный постулат предполагает, что формирование ε_s полностью совпадает с интервалом изменения тока, который на экспериментальных осциллограммах выделен временными курсорами как период полного закрытия транзистора и прекращения тока через него.
Настоящий эксперимент демонстрирует прямое нарушение этого принципа. Мощный импульс ЭДС с амплитудой ~1.5 кВ формируется строго после завершения изменения тока (dI/dt → 0), то есть в условиях, когда, согласно классической формуле и лежащему в её основе постулату, ЭДС должна быть равна нулю. Энергетический отклик системы не только не синхронен с dI/dt, но и отстаёт от него, имея собственную, на порядок большую длительность.
Ключевые экспериментальные наблюдения:
- Фазовая привязка. Момент начала формирования аномального отклика определяется типом используемого транзистора и жёстко привязан к времени его полного закрытия, а не к волновым свойствам системы.
- Независимость фазы от параметров цепи. Изменение индуктивности в цепи влияет на амплитуду и длительность формируемого импульса, но не сдвигает его фазу относительно момента завершения коммутации, что исключает доминирующую роль классического волнового процесса, время которого зависит от этих параметров.
- Временное несоответствие. Типичное время полного закрытия силового транзистора (18–50 нс) является более чем достаточным интервалом, в течение которого классическая ЭДС самоиндукции (как мгновенная реакция на di/dt) должна была бы полностью проявиться. Однако в течение этих 18–50 нс ожидаемый отклик отсутствует. Наблюдаемый мощный энергетический импульс возникает позже, что также противоречит объяснениям, сводящим эффект к простому волновому запаздыванию.
Экспериментально установленное временно́е разделение процессов ставит под сомнение не только количественную формулу, но и само определение феномена "самоиндукции" в его классической трактовке.
Если принять, что "ЭДС самоиндукции" по определению является прямым и синхронным противодействием изменению тока (следствием dI/dt), то наблюдаемое явление не может быть названо "ЭДС самоиндукции" в строгом смысле этого термина. Оно возникает в условиях dI/dt → 0 и ведёт себя как автономный процесс.
Это приводит к терминологическому парадоксу: мы наблюдаем мощный энергетический отклик индуктивной системы на коммутацию, который по всем внешним признакам (источник — энергия магнитного поля катушки, направление — против изменения тока) соответствует интуитивному пониманию "самоиндукции", но при этом нарушает её определение, закреплённое в формуле E = –L di/dt.
ЭДС самоиндукции - энергетический отклик электродинамической системы после завершения коммутации.
Опубликовано: 11/11/25
Экспериментально наблюдаемое рассогласование во времени между изменением тока di/dt, регистрируемым локально, и интегральным откликом в виде ЭДС на выводах катушки, указывает на то, что формула E = -L * di/dt, являющаяся следствием закона Фарадея становится неадекватной. Полученные данные свидетельствуют, что ЭДС самоиндукции в данном случае формируется как собственный, инерционный отклик распределённой электродинамической системы (включающей проводники, поля и паразитные реактивности) на резкое возмущение, что требует перехода от модели сосредоточенной индуктивности к полевой модели с распределёнными параметрами и конечным временем установления процесса.
- Под электродинамической системой или «физической средой» в данном контексте я понимаю не внешнее пространство, а саму распределённую электромагнитную систему эксперимента: проводники с их инерционными носителями заряда, паразитные ёмкости и индуктивности, а главное — энергия электромагнитного поля, локализованная вокруг элементов цепи. Именно эта «среда» демонстрирует инерционный, запаздывающий отклик на резкое возмущение.
- Под «откликом» я подразумеваю сложную, нелинейную и инерционную релаксацию этой самой распределённой системы, которая запускается резким возмущением и порождает эффекты, не описываемые моделью ε = -L di/dt. Именно это и является предметом исследования.
Методика эксперимента.
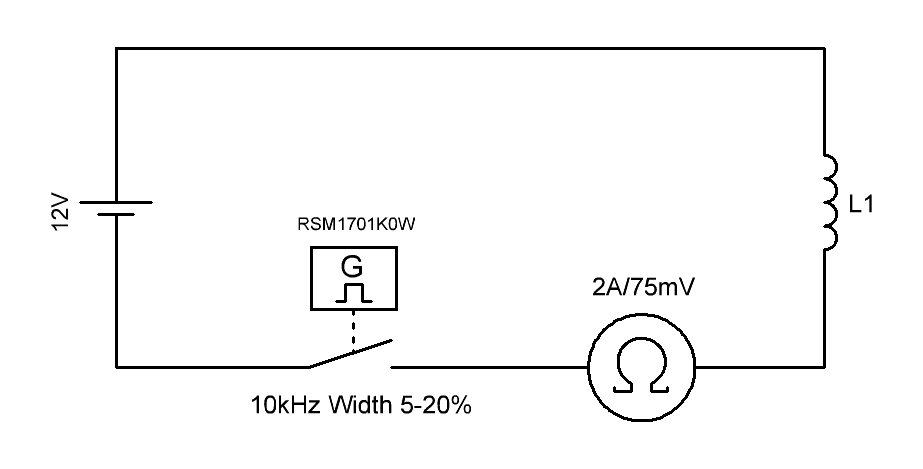
Экспериментальная установка представляет собой последовательную RL-цепь, содержащую:
- источник постоянного напряжения 12 В (аккумулятор);
- исследуемую катушку индуктивности c воздушным сердечником 70.98uH;
- измерительный шунт 2А/75мВ, подключен между индуктивностью и стоком транзистора;
- ключевой элемент (транзистор RSM1701K0W).
Регистрация сигналов осуществлялась цифровым осциллографом Siglent SDS1204X-E (200 МГц, 1 Гвыб/с) по двум каналам: первый канал (жёлтый луч) был подключен к затвору транзистора для фиксации момента коммутации, а второй канал (синий луч) — к измерительному шунту для контроля тока в цепи. Управляющие импульсы на затвор транзистора подавались с внешнего генератора UTG962E через специализированный драйвер TC4452. Амплитуда управляющего напряжения +15 В гарантировала режим глубокого насыщения транзистора до коммутации.
Результаты и наблюдения.
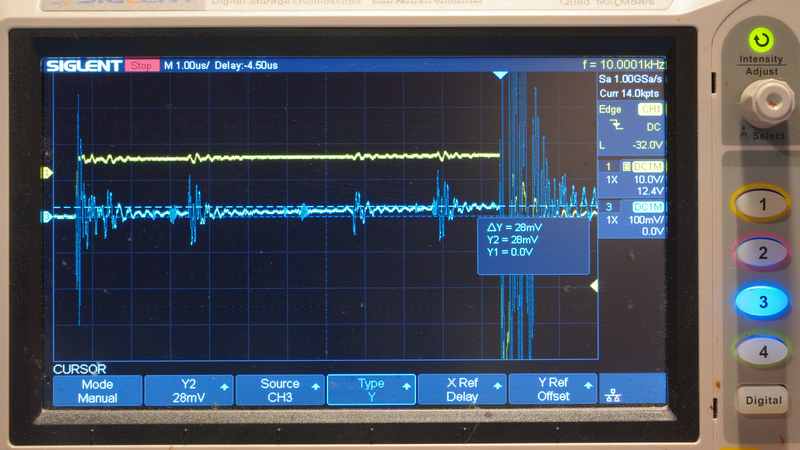
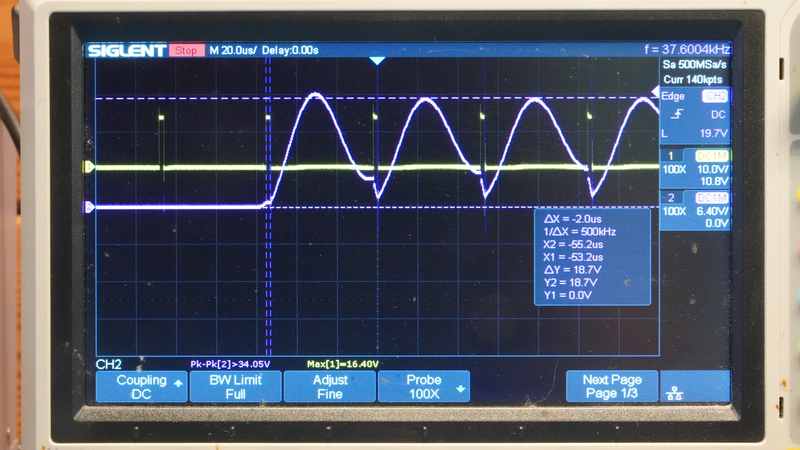
В интервале, когда транзистор открыт, сигнал напряжения на затворе транзистора U_GS (Канал 1, Жёлтый луч) сохраняет уровень +15 В, что соответствует режиму насыщения. Напряжение на измерительном шунте (Канал 3, Синий луч) демонстрирует линейный рост, характерный для процесса нарастания тока в RL-цепи при подаче постоянного напряжения. Непосредственно перед моментом коммутации t_0 зафиксировано напряжение на шунте 28.0 мВ. С учётом калибровочного коэффициента шунта 26.67 А/В установившееся значение тока составляет: 2.00 А. Наблюдаемая динамика и полученное значение тока согласуются с теоретической оценкой, основанной на напряжении источника и сопротивлении цепи, что подтверждает корректность работы измерительной системы на данном этапе.
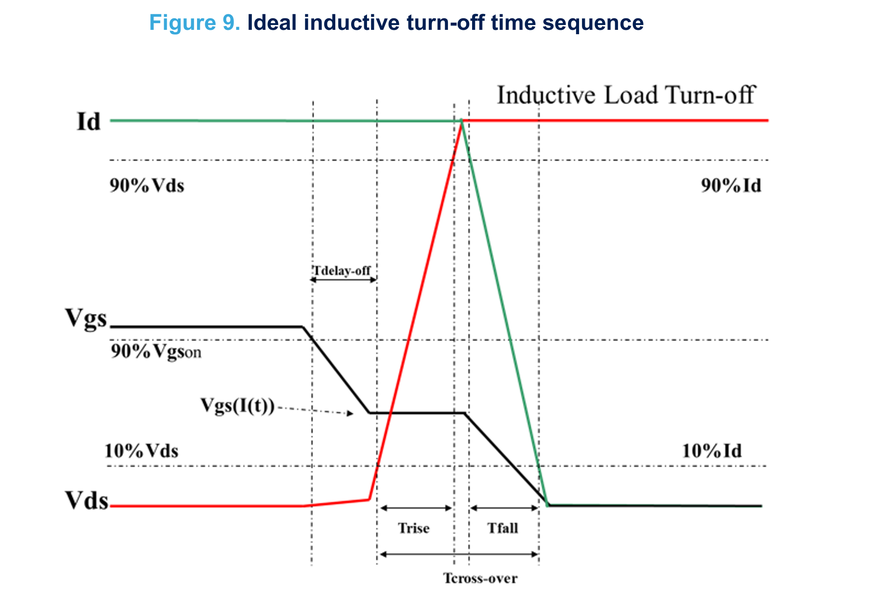
На рисунке далее представлена классическая модель работы транзистора с индуктивной нагрузкой. Согласно ей, ток через транзистор (зелёный луч) начинает убывать после прохождения плато Миллера и полностью прекращается, когда напряжение на затворе становится равным нулю.
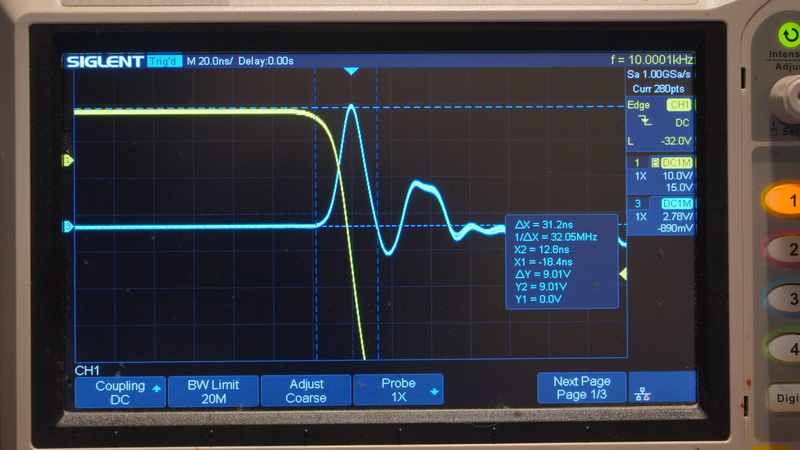
В ходе эксперимента в момент начала запирания транзистора (t = t_0) вместо монотонного спада был зафиксирован кратковременный высокоамплитудный импульс тока. На представленной осциллограмме детально показан данный переходный процесс.
Количественные параметры аномалии (стабильные и воспроизводимые):
- Амплитуда напряжения на измерительном шунте: U_shunt_peak = 9.0 В.
- Длительность импульса по уровню 0.5U_peak: τ_imp ≈ 31.2 нс.
- Расчетная амплитуда тока (с учетом коэффициента шунта k_sh = 26.67 А/В): I_peak = k_sh * U_shunt_peak ≈ 240.0 А.
Для экспериментальной демонстрации устойчивости и воспроизводимости эффекта аномального роста тока в галерее представлены осциллограммы (эпюры изменения тока на измерительном шунте) для различных типов силовых транзисторов..
Количественный анализ аномалии.
Кратковременный наносекундный всплеск тока в 240 А не вызывает немедленного разрушения ключевого элемента. Его главная опасность — электромагнитная: пробой изоляции, межвитковое перенапряжение в катушке, разрушение полупроводникового ключа.
Ключевое противоречие: Величина пикового тока I_peak более чем в 100 раз превышает установившееся значение в цепи перед коммутацией (I_0 ≈ 2.0 А). Обратите внимание: в момент, когда транзистор должен быть полностью закрыт по классической модели (V_GS = 0), осциллограмма фиксирует не ноль тока, а его максимальное значение.
Физическая интерпретация аномального всплеска.
Наблюдаемый всплеск принципиально несовместим с квазистационарной моделью сосредоточенной RL-цепи. Для интерпретации применима аналогия с гидравлическим ударом, где малое управляющее воздействие (закрытие клапана/ключа) высвобождает энергию, порождая мощный импульсный отклик (скачок давления/ЭДС).
Работы Н. Е. Жуковского, описывающие этот процесс формулой ΔP = ρ * c * Δv, указывают на фундаментальный принцип: между кинетической энергией потока, запасённой в системе до момента удара (~ρ * Δv), и энергией скачка давления, возникающей после него (~ρ * c * Δv), стоит знак не равенства, а преобразования с коэффициентом c. Энергия ударного импульса не содержится в явном виде в начальной кинетической энергии; она проявляется благодаря динамическим свойствам и упругости всей распределённой системы (труб, жидкости) в момент её резкого возмущения. Скорость ударной волны c выступает как коэффициент динамического усиления.
| Гидравлический удар (Н.Е. Жуковский) | Электромагнитный процесс (Эксперимент) |
|---|---|
| Мгновенная остановка потока клапаном Резкое внешнее возмущение (Δv/Δt → max) |
Наносекундное запирание транзистора Причина: резкое внешнее возмущение (tfall ~ 18 нс, dI/dt → max) |
| Кратковременный скачок давления (Δp) Локальный экстремум давления — прямая «ударная» волна |
Первичный всплеск тока до Ipeak ≈ 240 А Прямой отклик: локальный экстремум силы тока на возмущение |
| Распространение ударной волны и высокочастотные колебания давления Собственные резонансы упругой системы труба-жидкость |
Затухающие ВЧ-колебания тока (~18 нс) Быстрое следствие: «звон» (ringing) в паразитном LC-контуре |
| Медленная релаксация и перераспределение энергии в объёме Инерционная релаксация и диссипация энергии |
Длительный импульс ЭДС UL(t) (~180 нс) Медленное следствие: интегральный отклик распределённой системы |
Данная аналогия находит прямое отражение в экспериментальных данных::
- Максимум после закрытия: Как и в гидроударе (где скачок давления достигает максимума после того, как заслонка уже полностью закрыта), в эксперименте мощный импульс ЭДС и аномальный ток формируются после полного закрытия транзистора (V_GS = 0). Именно в этот момент, когда классическая модель предсказывает I = 0, осциллограмма фиксирует максимальный ток (~240 А) и начало импульса ЭДС. Совпадение моментов "закрытие ключа" – "максимум тока" является строгой параллелью с гидроударом ("закрытие заслонки" – "максимум давления").
- Автономный процесс:С этого момента процесс развивается автономно, определяясь внутренней динамикой системы. Роль «коэффициента усиления» c играют инерционные свойства носителей заряда и распределённый, волновой характер электромагнитной энергии.
- Перенос коэффициента c: В этой аналогии роль коэффициента динамического усиления c из формулы Жуковского играют инерционные свойства носителей заряда и распределённый, волновой характер электромагнитной энергии в системе. Ключевой вывод заключается в том, что именно эти динамические свойства системы, а не энергия, изначально запасённая в магнитном поле индуктивности (½LI₀²), определяют, насколько мощным будет "удар" (амплитуда импульса) после срабатывания триггера..
Важным экспериментальным подтверждением применимости данной аналогии служит установленная зависимость: более резкое прекращение потока (уменьшение времени запирания транзистора) закономерно увеличивает амплитуду импульса, а не ускоряет релаксацию. Следовательно, скорость коммутации определяет пиковую энергию переходного процесса, что прямо противоречит предсказаниям классической модели.
Энергетические последствия и полевая динамика.
Основу описания электромагнитных процессов в сплошной среде составляют уравнения Максвелла и материальные уравнения (соотношения), связывающие векторы полей. Для линейной, изотропной и недиспергирующей среды они имеют вид:
1. Для электрического поля:
D = ε * E,
где:
- D — вектор электрической индукции (электрическое смещение),
- ε = ε₀ * ε_r — абсолютная диэлектрическая проницаемость среды,
- ε₀ — диэлектрическая постоянная вакуума,
- ε_r — относительная диэлектрическая проницаемость среды (для вакуума ε_r = 1),
- E — вектор напряжённости электрического поля.
2. Для магнитного поля:
B = μ * H,
где:
- B — вектор магнитной индукции,
- μ = μ₀ * μ_r — абсолютная магнитная проницаемость среды,
- μ₀ — магнитная постоянная,
- μ_r — относительная магнитная проницаемость среды (для вакуума и воздуха μ_r ≈ 1),
- H — вектор напряжённости магнитного поля.
Динамика процесса определяется связью тока смещения со скоростью изменения электрического поля. Ток смещения Jсм определяется как производная по времени от вектора D:
J_см = ∂D/∂t.
Подстановка материального уравнения даёт прямую связь:
J_см = ∂(εE)/∂t = ε * (∂E/∂t).
Это соотношение является центральным для понимания механизма распространения возмущения при резкой коммутации. Быстрое изменение поля ∂E/∂t в точке разрыва тока порождает ток смещения в окружающем пространстве, что позволяет электромагнитному возмущению распространяться без движения свободных зарядов — за счёт упругой перестройки самого поля. Резкая коммутация создаёт в распределённой системе скачок импеданса, выступая как граничное условие для уравнений Максвелла. Их решения предсказывают волновое распространение возмущения со скоростью света и возможность усиления полей при отражениях, что представляет собой прямой электродинамический аналог формирования ударной волны. Таким образом, адекватным «уравнением состояния» для системы в таких условиях являются сами уравнения Максвелла, а не феноменологическое соотношение для сосредоточенной индуктивности.
Максвелл создавал свою теорию в рамках концепции механического эфира — всепроникающей упругой среды, колебания и напряжения в которой и проявлялись как электрические и магнитные явления, где поля E и H описывали механические напряжения и смещения. Поэтому предлагаемая аналогия с гидроударом Жуковского — это не просто образ для упрощения, а возвращение к пониманию единого принципа: образования ударной волны в упругой среде при её резком возмущении. Электродинамический удар и гидроудар представляют собой частные проявления этого общего принципа в средах с разными физическими свойствами (описываемых константами ε,με,μ для поля и ρ,Kρ,K для жидкости).
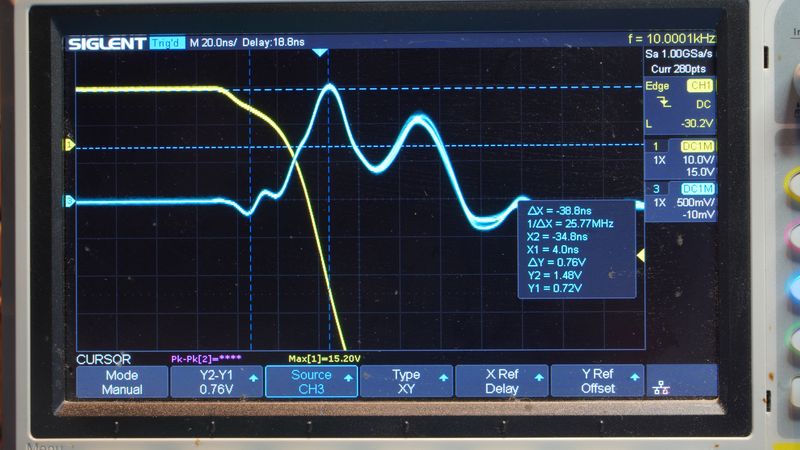
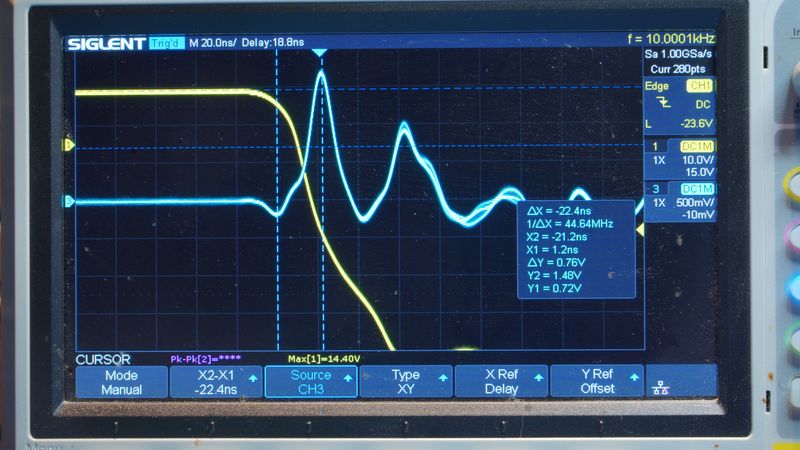
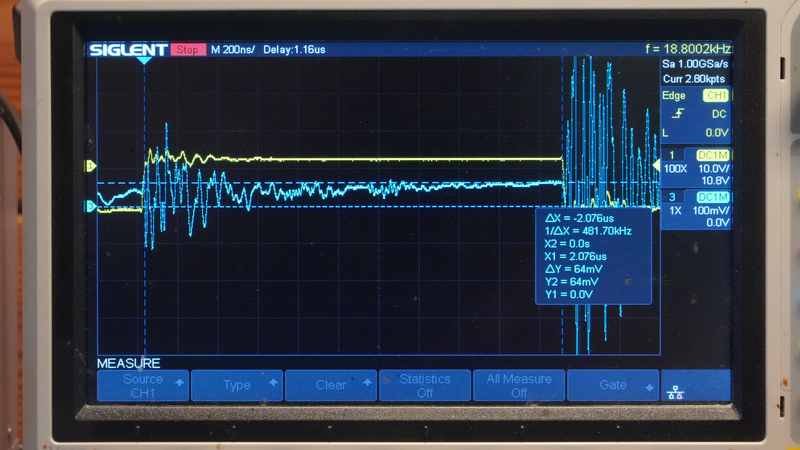
Ключевым результатом данной работы является экспериментально установленное отсутствие временной корреляции между прямым измерением напряжения на выводах катушки, интерпретируемым как ЭДС самоиндукции, и сигналом пробной катушки, пропорциональным скорости изменения магнитного потока (∂Φ/∂t) в ближней зоне. Для наглядности результаты представлены на осциллограммах
- Бордовый луч: регистрирует напряжение на индуктивности, интерпретируемое как ЭДС самоиндукции (положительная полярность, длительность ≈219 нс).
- Синий луч (пробная катушка): фиксирует сигнал, пропорциональный скорости изменения магнитного потока (∂Φ/∂t) вблизи исследуемой катушки.
Хотя ферритовый сердечник пробного датчика вносит неконтролируемый фазовый сдвиг, что исключает прямое сравнение фаз сигналов, ключевым фактом является порядковое расхождение в их временны́х масштабах. Длительность импульса с пробной катушки, отражающего локальные изменения поля, составляет ~18 нс, более чем в десять раз меньше длительности импульса ЭДС самоиндукции (~180 нс).
Этот факт служит прямым экспериментальным свидетельством разделения доминирующих физических механизмов в переходном процессе. Генерация вихревого электромагнитного поля в пространстве (отклик пробной катушки) и формирование напряжения на выводах катушки (измеренная ЭДС) оказываются разнесёнными во времени процессами различной физической природы.
Объяснить данное рассогласование в рамках классической модели сосредоточенных элементов (RL-цепи) невозможно. В этой модели энергия жёстко ограничена запасом ½LI₀², а процессы во всех элементах цепи предполагаются синхронными. В реальной распределённой системе энергия поля способна к перераспределению, что приводит к возникновению локальных концентраций («ударов»), мощность которых определяется волновой динамикой среды, а не исходным током. Таким образом, классическая модель с сосредоточенной индуктивностью (основанная на E = -L di/dt) оказывается неприменимой для описания наблюдаемого аномального переходного процесса.
Следовательно, наблюдаемая динамика требует перехода к модели открытой распределённой электродинамической структуры. В такой модели энергетический отклик (аномальный ток и ЭДС) определяется не параметрами сосредоточенных элементов L и R, а внутренними волновыми свойствами самой системы. Резкая коммутация выступает в роли триггера, переводящего систему в качественно иной режим с волновым усилением, что и объясняет наблюдаемое аномальное превышение мощности.
Энергетический парадокс и его исторический контекст.
Обнаруженная закономерность выявляет фундаментальный парадокс: пиковая сила тока I_peak в момент разрыва цепи не только превышает его установившееся значение до коммутации, но и возрастает с уменьшением времени запирания ключа (t_fall).
Данное явление было эмпирически обнаружено и использовано Н. Теслой. Ключевой целью его инженерных поисков, включавших разработку быстрых искровых разрядников, было не просто прервать ток, а осуществить этот разрыв максимально резко, чтобы инициировать и усилить сам токовый всплеск в момент коммутации. Вызванный таким образом лавинообразный рост плотности носителей заряда в узле разрыва и являлся первичным источником для последующей генерации мощных импульсных разрядов высокой энергии.
Таким образом, настоящие эксперименты количественно воспроизводят на современной элементной базе физический принцип, лежавший в основе этих исторических исследований: контролируемое создание экстремально крутого фронта прерывания тока (di/dt) для индукции вторичного токового всплеска, мощность которого определяется не исходной энергией цепи, а скоростью её коммутации. Это прямо указывает на существование порогового режима работы импульсных систем, при котором энергоэффективность процесса определяется нелинейной зависимостью от скорости переключения, что выходит за рамки описания классической моделью сосредоточенных элементов.
Безусловно, в процессе запирания транзистора ток в цепи обязан уменьшаться от установившегося значения (~2 А) до нуля согласно классической модели RL-цепи. Однако на представленной осциллограмме этот плавный спад не виден по причине, связанной с выбором масштаба измерений: для детального наблюдения аномального всплеска (~240 А) осциллограф был настроен на высокий коэффициент усиления (чувствительность ~9 В на весь экран). При такой настройке малый сигнал установившегося тока (~28 мВ, что соответствует 2 А) находится на уровне собственного шума, и динамика его изменения не наблюдаема.
Прямая аналогия с гидроударом помогает понять это разделение процессов. При закрытии заслонки поток воды через неё также уменьшается до нуля, но это медленное уменьшение не отменяет одновременного возникновения ударной волны с аномально высоким давлением в системе. Эти два процесса — плавное уменьшение потока и ударный скачок — существуют одновременно, но в разных временных и энергетических масштабах.
Точно так же и в нашем эксперименте: классическое уменьшение тока через транзистор (аналог потока) не исключает одновременного возникновения электродинамического удара — процесса концентрации энергии в точке разрыва с образованием токового всплеска до 240 А (аналог скачка давления). Осциллограмма, сфокусированная на наносекундном масштабе, фиксирует именно этот ударный процесс, который и является предметом нашего исследования.
Установленная физическая аналогия между гидроударом и электродинамическим ударом подчёркивает не только их общую природу, но и схожие инженерные последствия. Подобно тому, как гидроудар представляет опасность для трубопроводов и требует мер по его гашению, резкое прекращение тока в распределённых электродинамических системах может приводить к пробою изоляции, выходу из строя компонентов и электромагнитным помехам. Однако, если классический инженерный подход направлен на подавление таких явлений, настоящее исследование открывает иной путь: не гасить, а контролируемо использовать высвобождаемую в процессе удара концентрированную энергию.
Переосмысление термина «самоиндукция»
Представленные экспериментальные данные побуждают вернуться к исходному смыслу термина «самоиндукция» — самостоятельная, независимая, автономная индукция. Наблюдаемое рассогласование во времени между изменением тока и генерируемой ЭДС указывает на то, что в переходном процессе ЭДС возникает не как прямое и мгновенное следствие изменения тока (di/dt), а как самостоятельный отклик распределённой электродинамической системы на возмущение.
Превышение работы ЭДС самоиндукции над
затратами источника питания.
Опубликовано: 06/01/26
Аннотация.
В работе представлены результаты экспериментального исследования энергетического баланса при резкой коммутации RL-цепи с демпфирующим конденсатором, включённым параллельно ключевому транзистору. Классическое описание коммутации индуктивности в идеальном LC-контуре предполагает, что энергия ΔWC, полученная конденсатором, не превышает энергии магнитного поля WL, накопленной к моменту разрыва цепи. В ходе эксперимента (L = 70 мкГн, C = 1 мкФ, I₀ = 0.853 А) было выполнено прямое сравнение этих величин. Установлено, что энергия ΔWC = 175 мкДж, переданная конденсатору первым импульсом ЭДС самоиндукции, в 6.86 раза превышает начальную энергию WL = 25.5 мкДж. Целью работы является анализ причин этого фундаментального расхождения с классическим представлением и определение физики процесса, лежащего в основе передачи энергии.
Введение.
Согласно классическому подходу, источник питания создаёт ток, запасая энергию в магнитном поле катушки (WL = ½ L I02). Затем, при размыкании цепи, энергия магнитного поля является источником энергии, которая формирует заряд конденсатора.
Когда вы вращаете ручку динамомашины, вы не переносите физическое усилие в электрический ток, а запускаете процесс генерации электрической энергии. Аналогично, прерывание тока через индуктивность запускает процесс, в котором вихревое электрическое поле (количественно описываемое ЭДС самоиндукции) становится источником работы по формированию заряда. Это прямо следует из законов электродинамики: работа по формированию заряда конденсатора совершается исключительно этим полем. Следовательно, величина совершённой работы (и конечная энергия ΔWC) определяется не энергией WL, а параметрами, которые задают само поле: током I0 в момент коммутации и скоростью его изменения dI/dt.
Таким образом, классическое равенство ΔWC = WL является ошибочным по своей сути: оно пытается приравнять энергию состояния системы (WL) к энергии, генерируемой процессом её изменения (ΔWC).
Целью данной работы является экспериментальная демонстрация этого принципа. В работе показано, что энергия ΔWC, сгенерированная первым импульсом ЭДС самоиндукции при резкой коммутации, многократно превышает исходную энергию WL. Для чистоты эксперимента использована схема, позволяющая измерить работу, совершённую исключительно вихревым электрическим полем индукционного отклика.
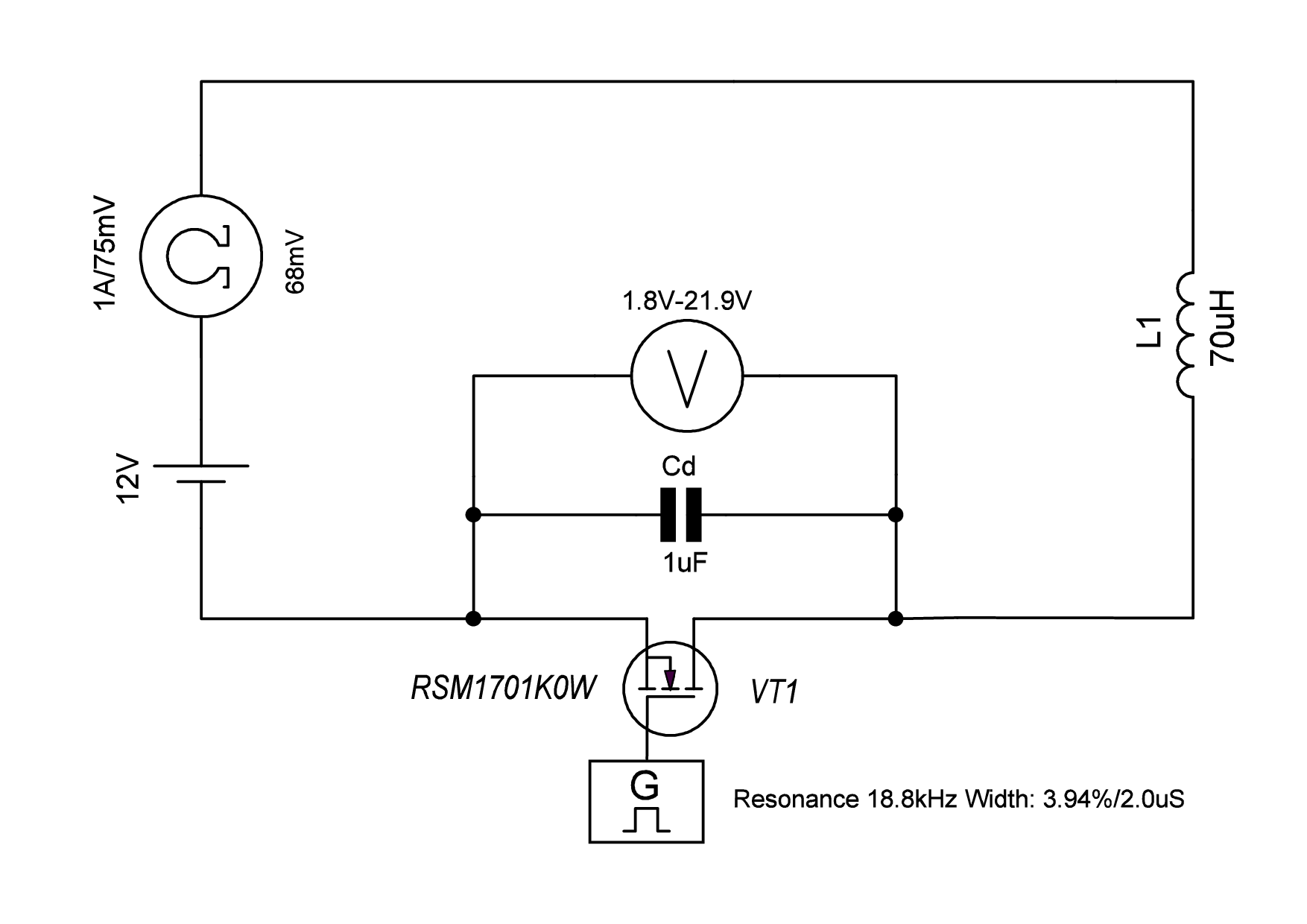
Экспериментальная установка.
Принципиальная схема экспериментальной установки, представленная на рисунке, была собрана для исследования энергетического баланса при резкой коммутации тока в индуктивности. Схема представляет собой последовательную RL-цепь, в которой в качестве ключа используется мощный MOSFET-транзистор, а параллельно ему подключён демпфирующий конденсатор Cd.
Состав установки:
- Нагрузка: Соленоид с воздушным сердечником. Индуктивность, измеренная LCR метром MS5308, составила L = 70 мкГн.
- Ключевой элемент: Мощный N-канальный MOSFET (RSM1701K0W, G3R350MT12D, AIMZH120R060M) с низким сопротивлением открытого канала RDS(on) для минимизации потерь в фазе накопления тока и минимальным временем выключения (tfall) для обеспечения максимальной скорости изменения тока dI/dt в момент коммутации.
- Демпфирующий накопитель: Плёночный конденсатор Cd = 1.0 мкФ ±5%, включённый непосредственно между стоком и истоком транзистора для накопления энергии, генерируемой импульсом ЭДС самоиндукции.
- Система управления: Генератор прямоугольных импульсов UTG962E и драйвер TC4452, с гальванической развязкой для формирования фронта управляющего сигнала с минимальным временем нарастания и спада.
- Источник питания: Стабилизированный источник постоянного тока HSPY-400-01 с выходным напряжением VCC = 12 В. Для проверки независимости результата от типа источника дополнительно использовался аккумулятор MF85D23 (VCC = 12 В).
- Средства измерений: Прецизионный шунт сопротивлением Rш = 0.075 Ом для измерения тока IL(t). Цифровой осциллограф SDS1204X-E (полоса 200 МГц, частота дискретизации 1 Гвыб/с) для синхронной регистрации напряжения на шунте Uш(t) и напряжения на конденсаторе UC(t).
Методика измерений и настройка режима.
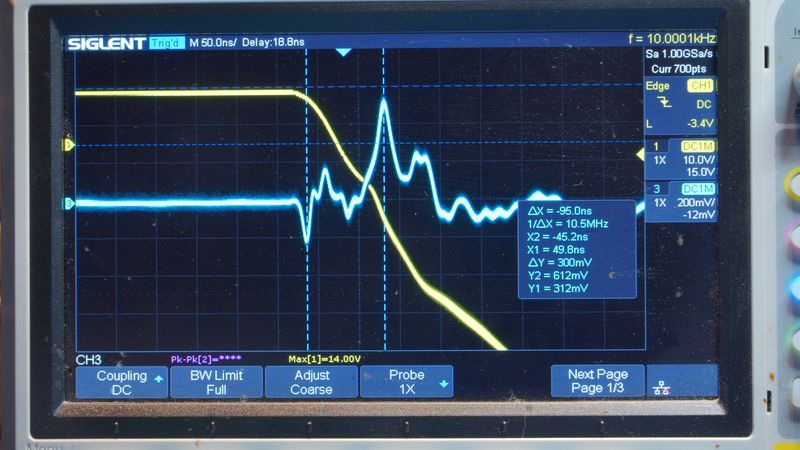
Ключевым этапом являлась настройка частоты следования импульсов frep в резонанс с собственными колебаниями контура, образованного индуктивностью L и конденсатором Cd после размыкания ключа.
Для возбуждения использовалась последовательность прямоугольных импульсов с длительностью открытого состояния ключа ton = 2.0 мкс, достаточной для полного разряда демпфирующего конденсатора Cd к моменту начала каждого цикла.
Расчётная резонансная частота контура:
f0 calc = 1 / (2π√(LCd)) ≈ 1 / (2π√(70·10-6 · 1·10-6)) ≈ 19.0 кГц.
Экспериментально, путём регулировки frep, был достигнут минимум потребления при частоте f0 exp = 18.8 кГц. Хорошее соответствие расчётного и экспериментального значений (расхождение ~1%) подтверждает корректность измеренных параметров элементов и доминирование идеальной LC-модели в динамике процесса после коммутации.
Фазовый анализ процесса.
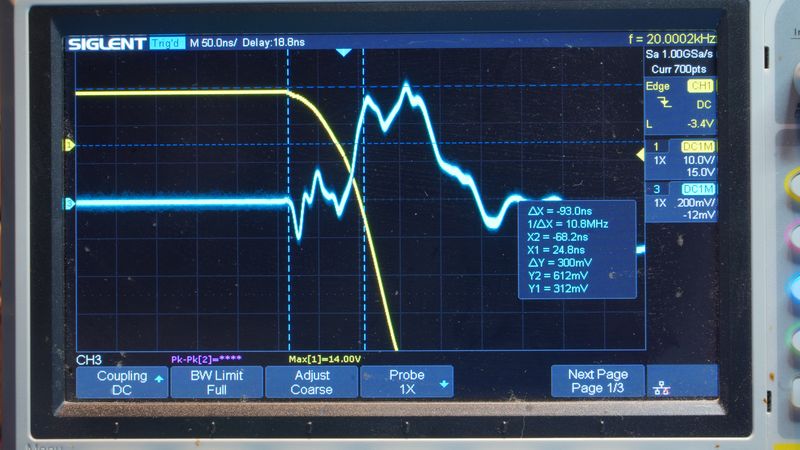
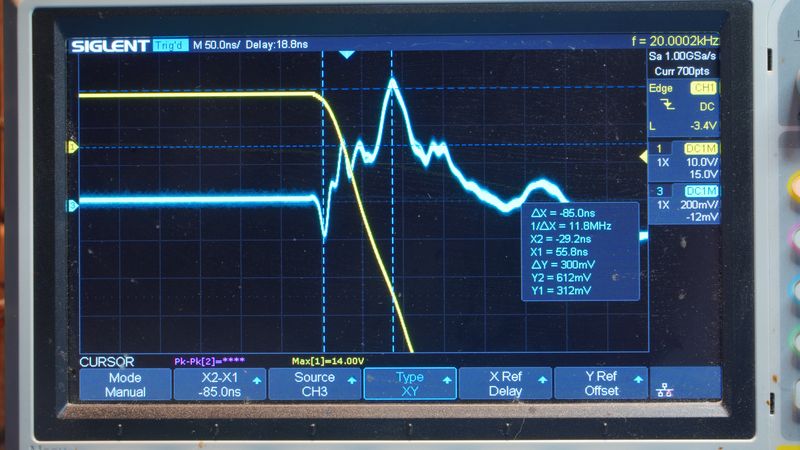
Работа установки представляет собой повторяющийся цикл, который можно разделить на три последовательные фазы, определяемые состоянием ключа S1 (MOSFET). На рисунке представлена осциллограмма напряжения UC(t), иллюстрирующие этот цикл.
- Принудительный разряд конденсатора (ton_start < t < ton_end, ключ открыт). При открытии транзистора конденсатор Cd, заряженный в предыдущем цикле, разряжается через его низкоомный канал. Длительность открытого состояния ton = 2.0 мкс выбрана с большим запасом относительно постоянной времени разряда τразр = RDS(on)Cd. Это гарантирует выполнение к концу фазы критического условия: UCton_end ≈ 0 В. Ток через индуктивность L в этой фазе пренебрежимо мал.
- Линейное накопление тока и энергии (ton_end < t < toff, ключ открыт). После завершения разряда Cd через индуктивность L от источника питания VCC протекает линейно нарастающий ток: IL(t) ≈ (VCC / L) · t. К моменту коммутации toff ток достигает амплитудного значения I0. Источником энергии в этой фазе является источник питания VCC, а её результатом — запас энергии WL = ½ L I02 в магнитном поле индуктивности.
- Генерация импульса ЭДС и колебаний (t ≥ toff, ключ разомкнут). В момент toff ключ резко размыкается, что в соответствии с законом Ɛ = –L (dIL/dt) порождает в индуктивности импульс ЭДС самоиндукции. Поскольку цепь с источником питания разорвана, а конденсатор Cd в начале фазы разряжен (UC = 0), ЭДС самоиндукции становится единственной сторонней силой в образовавшемся последовательном LC-контуре. Она совершает работу по перемещению заряда, вызывая заряд конденсатора до амплитудного значения UCmax и инициируя затухающие колебания. Первая четверть периода этих колебаний представляет собой непосредственный результат работы импульса ЭДС по передаче энергии конденсатору.
Результаты измерений и расчёт.
Анализ проводится для первого размыкания ключа после включения источника питания. На фотографиях представлены осциллограммы, соответствующие первому циклу заряда конденсатора: напряжение на нём UC(t) и ток через индуктивность IL(t), измеряемый по падению напряжения на прецизионном шунте.
Ключевые измеренные параметры цикла:
- Напряжение на конденсаторе в начале коммутации: UC(toff) ≈ 0 В.
- Ток через индуктивность перед коммутацией: Амплитуда напряжения на шунте составила Uш = 64.0 мВ. Следовательно, ток составлял I0 = Uш / Rш = 64.0 мВ / 0.075 Ом = 0.853 А.
- Максимальное напряжение на конденсаторе от первого импульса ЭДС: В первой четверти периода колебаний зафиксирован первый максимум UCmax = 18.7 В.
Энергетическая интерпретация и расчёт: Поскольку в начале фазы генерации (t = toff) конденсатор был разряжен, а ключ разомкнут, единственной сторонней силой, совершающей работу по заряду конденсатора в течение первой четверти периода, является импульс ЭДС самоиндукции. Следовательно, энергия, переданная конденсатору этим импульсом, равна энергии, запасённой в его электрическом поле к моменту достижения UCmax: ΔWC = ½ Cd UCmax2 = ½ × 1.0×10-6 Ф × (18.7 В)2 ≈ 1.75×10-4 Дж (175 мкДж).
Энергия, которая была запасена в магнитном поле индуктивности к моменту разрыва цепи, составляет: WL = ½ L I02 = ½ × 70×10-6 Гн × (0.853 А)2 ≈ 2.55×10-5 Дж (25.5 мкДж).
Фундаментальный результат: Переданная конденсатору энергия ΔWC превышает первоначально запасённую в индуктивности энергию WL в ΔWC / WL ≈ 6.86 раза.
Физическая интерпретация результата.
Классическая интерпретация, приводимая в учебных курсах, сводится к равенству энергий: WC_max = WL = ½ L I02. Настоящий эксперимент демонстрирует принципиальную неадекватность такого подхода для описания процесса при резкой коммутации.
Согласно фундаментальному закону электромагнитной индукции, ЭДС самоиндукции определяется не запасённой энергией магнитного поля, а скоростью изменения порождающего это поле тока:
Ɛ = –L (dI/dt)
Таким образом, сила электромагнитного отклика системы задаётся динамическими параметрами коммутации: величиной тока I0 в момент разрыва и, что критически важно, скоростью его изменения dI/dt. Энергия магнитного поля WL = ½ L I02 является лишь одним из необходимых условий, но не определяет энергию возникающего импульса ЭДС.
Для корректного понимания необходимо чётко разграничить физическую природу двух полей, участвующих в процессе:
- Магнитное поле, создаваемое током проводимости I0. Его величина пропорциональна току I, а источником является движущийся заряд. Энергия, запасённая в объёме этого поля к моменту коммутации, составляет WL = ½ L I02.
- Изменение тока (dI/dt) в момент разрыва цепи формирует вихревое электрическое поле (электромагнитный отклик). Это поле описывается законом Фарадея: rot E = –∂B/∂t. Его интегральным проявлением для контура служит ЭДС самоиндукции: Ɛ = –L (dI/dt). Именно эта ЭДС, будучи сторонней силой в цепи, совершает работу по формированию заряда конденсатора.
Эти два поля имеют разную физическую природу и источник. Магнитное поле порождено током (движением зарядов). Импульсное электрическое поле порождено изменением этого тока (dI/dt).
Следовательно, энергия WL, запасённая источником питания, служит лишь необходимым условием — триггером, запускающим процесс. Энергия же ΔWC, измеренная на конденсаторе, является мерой работы импульса вихревого электрического поля — электромагнитного отклика системы на резкое прекращение тока.
Из этого следует важное наблюдение: при одной и той же величине WL система с иными параметрами (например, с большей индуктивностью L и меньшим током I0) даст импульс ЭДС меньшей амплитуды и, как следствие, меньшую величину ΔWC. И наоборот, система с меньшей L и большим I0 при том же WL приведёт к большему ΔWC. Это однозначно доказывает, что решающим фактором для конечного результата (ΔWC) является не интегральная энергия WL, а конкретное значение тока I0 в момент разрыва и скорость его изменения dI/dt, определяемая динамикой ключа.
Заключение.
В ходе экспериментального исследования энергетического баланса при резкой коммутации RL-цепи с демпфирующим конденсатором получены прямые измерения энергии, передаваемой конденсатору первым импульсом ЭДС самоиндукции (ΔWC), и энергии, запасённой в магнитном поле индуктивности (WL). Установлено, что в исследованной конфигурации энергия ΔWC = 175 мкДж превышает энергию WL = 25.5 мкДж в 6.86 раза.
Данный результат является прямым экспериментальным доказательством того, что энергия импульса ЭДС самоиндукции не равна и может многократно превышать энергию магнитного поля. Это опровергает упрощённую классическую модель, основанную на равенстве WL = ΔWC.
Физической основой этого явления служит то, что прерывание тока запускает качественно иной, автономный процесс. Быстрое изменение тока при разрыве цепи порождает вихревое электрическое поле (Ɛ = –L dI/dt), которое и совершает работу по заряду конденсатора. Таким образом, энергия ΔWC является мерой работы этого автономного поля, в то время как WL характеризует лишь состояние поля, созданного самим током I0.
Следовательно, определяющими параметрами для ΔWC выступают динамические характеристики коммутации — ток I0 и, прежде всего, скорость его изменения dI/dt. Импульс ЭДС — это не «переливание» энергии, а автономный генеративный процесс, энергетический потенциал которого определяется динамикой разрыва цепи, а не величиной первоначального запаса энергии.
Таким образом, полученные результаты указывают на необходимость пересмотра упрощённых энергетических моделей коммутации индуктивностей в инженерной практике и учебных курсах. Акцент должен смещаться с анализа интегральных величин (WL) на анализ динамических и волновых процессов в силовых цепях, которые в реальности определяют уровень коммутационных перенапряжений, энергетические потери и потенциальные возможности энергопреобразования.
Расчётное обоснование неадекватности E = –L di/dt.
Опубликовано: 07/12/25
Для прямой проверки соответствия экспериментальных данных классическому соотношению E = –L (di/dt)
был проведён расчёт ожидаемых временных параметров на основе измеренных величин.
Исходные экспериментальные данные:
- Индуктивность катушки: L = 79.98 мкГн
- Падение напряжения на токовом шунте (2 A / 75 мВ): U_ш = 28 мВ
- Ток в цепи перед коммутацией: I = U_ш / (75 мВ / 2 A) = 28 мВ / 0.0375 В/А ≈ 0.747 А
- Изменение тока при коммутации: ΔI ≈ 0.747 А (считая спад до нуля)
- Пиковая амплитуда импульса ЭДС: E_peak = 1458 В
- Измеренная длительность фронта закрытия транзистора: τ_комм = 18 нс
- Измеренная длительность импульса ЭДС: τ_имп = 184 нс
Расчёт по классической модели:
Если предположить, что наблюдаемая ЭДС (E_peak) является прямым следствием изменения тока (ΔI) за время коммутации (τ_комм) согласно формуле E_peak = L * (ΔI / Δt), то можно вычислить ожидаемую амплитуду:
E_расч = L * (ΔI / τ_комм) = 79.98e-6 Гн * (0.747 А / 18e-9 с) ≈ 3318 В
Расчётное значение (≈3318 В) более чем в 2.2 раза превышает экспериментально измеренную амплитуду (1458 В).
Обратный расчёт: определим время Δt_треб, за которое изменение тока ΔI должно произойти, чтобы по формуле E = L*(ΔI/Δt) получить измеренную амплитуду E_peak:
Δt_треб = L * ΔI / E_peak = 79.98e-6 Гн * 0.747 А / 1458 В ≈ 41.0 нс
Вывод количественного анализа:
Прямое применение классической формулы E = –L (di/dt) приводит к двум взаимоисключающим противоречиям с экспериментом:
- По амплитуде: Если подставить реальное di/dt (из ΔI и τ_комм), формула предсказывает импульс более 3300 В, чего нет.
- По времени: Если исходить из измеренной амплитуды ЭДС, формула требует, чтобы изменение тока длилось ~41 нс, что не соответствует фактам.
- По динамике: Формула связывает ЭДС с мгновенной скоростью изменения тока. Однако в эксперименте мощный энергетический процесс (длительностью 184 нс) начинается после завершения короткого (18 нс) события изменения тока.
Это однозначно свидетельствует, что пиковая ЭДС в 1458 В не является прямым и мгновенным следствием
изменения тока через индуктивность за время τ_комм = 18 нс. Классическая модель не способна
количественно описать ни амплитуду, ни, что более важно, временну́ю динамику наблюдаемого процесса
генерации ЭДС самоиндукции.
Несостоятельность энергетической модели самоиндукции.
Опубликовано: 25/12/25
В текущем разделе представлены результаты эксперимента, демонстрирующие отсутствие прямой зависимости амплитуды ЭДС самоиндукции от энергии, запасённой в магнитном поле катушки. На основании проведённых измерений сделан вывод о полной энергетической автономии процесса генерации ЭДС от традиционных источников энергии в системе.
Методика эксперимента.
Для количественной проверки гипотезы о независимости ЭДС самоиндукции от энергии магнитного поля были проведены серии измерений на соленоидах с воздушным сердечником. Исследовались катушки, намотанные проводом сечением 2.5 мм², двух типоразмеров (диаметром 83 мм и 130 мм) в диапазоне индуктивностей от 58.31 до 306.70 мкГн. Использование воздушного сердечника позволило исключить влияние магнитных потерь и нелинейных эффектов ферромагнетиков.
Экспериментальная установка была собрана по последовательной схеме, включающей:
- источник постоянного напряжения 12 В (аккумулятор);
- измерительный шунт с коэффициентом 2 А / 75 мВ;
- исследуемая катушка индуктивности;
- ключевой элемент (транзистор RSM1701K0W).
Управляющие импульсы на затвор транзистора подавались с внешнего генератора UTG962E через специализированный драйвер TC4452. Амплитуда управляющего напряжения +15 В гарантировала режим глубокого насыщения транзистора до коммутации. Измерения проводились двухканальным осциллографом: первый канал регистрировал ЭДС самоиндукции на выводах катушки, второй — падение напряжения на шунте для точного определения тока.
Принцип работы схемы.
При подаче управляющего импульса на транзистор, ключ закрывается, и через цепь (источник - шунт - катушка - ключ) начинает линейно нарастать ток, запасая энергию в магнитном поле катушки. После закрытия ключа (обрыв цепи) возникает импульс ЭДС самоиндукции значительной амплитуды.
Процедура измерений:
- Установка порога: Для каждой катушки ток плавно увеличивался до момента, когда амплитуда ЭДС самоиндукции достигала строго заданного значения — 1.0 кВ.
- Фиксация параметров:При достижении этого порога фиксировались установившийся ток (I), время накопления энергии и длительность импульса ЭДС.
- Сравнительный анализ:Все катушки сравнивались при идентичном выходном параметре — амплитуде ЭДС 1.0 кВ.
Осциллограмма процесса накопления энергии и коммутации..
На фотографии представлена осциллограмма, иллюстрирующая полный цикл работы системы. Желтый луч (канал 1) соответствует управляющему импульсу на затворе транзистора. Его передний фронт приводит к открытию ключа и началу фазы накопления энергии, в течение которой ток (синий луч, канал 2) линейно нарастает. Момент времени t₂ фиксирует амплитуду установившегося тока I непосредственно перед коммутацией.
Данная осциллограмма подтверждает корректность методики измерений и обеспечивает точность фиксации экспериментальных данных, представленных в таблице.
| L, мкГн | Диаметр катушки, мм | Ток I, А | ЭДС Es, кВ | Энергия W, мкДж | Время накопления тока, мкс | Длительность импульса ЭДС, нс |
|---|---|---|---|---|---|---|
| 58.31 | 83 | 1.107 | 1.0 | 35.7 | 4.88 | 160 |
| 94.49 | 83 | 0.867 | 1.0 | 35.5 | 6.36 | 200 |
| 284.1 | 83 | 0.440 | 1.0 | 27.5 | 11.08 | 384 |
| 64.78 | 130 | 0.337 | 1.0 | 3.7 | 5.48 | 172 |
| 136.87 | 130 | 0.133 | 1.0 | 1.2 | 7.48 | 240 |
| 306.70 | 130 | 0.400 | 1.0 | 24.5 | 11.6 | 384 |
Ток: I = Uшунта × 26.667 А/В
Энергия: W = (L × I²) / 2
Ток измеренный на шунте (I_shunt), — это единственный ток в последовательной цепи. Следовательно, рассчитанная энергия W = (L * I_shunt²)/2 — это уже интегральная величина. Она включает в себя энергию, запасённую в магнитном поле катушки и все омические потери в обмотке и на открытом ключе за время накопления. Таким образом, величина W является полной мерой энергозатрат от источника, необходимых для перевода системы в состояние, из которого возможна генерация ЭДС в 1 кВ.
Зависимость энергозатрат от диаметра катушки.
| Диаметр катушки, мм | Индуктивность, мкГн | Энергозатраты (W), мкДж |
|---|---|---|
| 83 | 58.31 | 35.7 |
| 94.49 | 35.5 | |
| 284.10 | 27.5 | |
| 130 | 64.78 | 3.7 |
| 136.87 | 1.2 | |
| 306.70 | 24.5 |
- Катушки диаметром 130 мм демонстрируют значительно меньшие энергозатраты при схожих индуктивностях
- Максимальная эффективность достигнута при диаметре 130 мм и L = 136.87 мкГн
- Разница в энергозатратах достигает 29.6 раз в пользу большего диаметра
Отсутствие корреляции ЭДС самоиндукции
и энергии магнитного поля.
Проведённые измерения выявили фундаментальную закономерность: при фиксированной амплитуде ЭДС самоиндукции в 1.0 кВ энергия, запасённая в магнитном поле катушки (W = L·I²/2), варьировалась в широких пределах — от 1.2 до 35.7 мкДж.
Классическая модель предполагает однозначную связь между амплитудой ЭДС самоиндукции и энергией, затрачиваемой источником питания. Согласно этой концепции, для генерации идентичных импульсов ЭДС амплитудой 1.0 кВ требуются соизмеримые энергозатраты, аккумулируемые в магнитном поле катушки.
Эксперимент выявил фундаментальное противоречие: при идентичной амплитуде ЭДС 1.0 кВ энергия магнитного поля варьируется в 30 раз (1.2-35.7 мкДж). Такой разброс исключает погрешность измерений и опровергает классическую модель, связывающую ЭДС самоиндукции с энергией источника. Результаты свидетельствуют о существовании альтернативного механизма генерации, не описываемого традиционной электродинамикой.
ЭДС самоиндукции и энергия магнитного поля.
Анализ зависимости эффективности t_имп/W (где t_имп — длительность импульса ЭДС) от энергии магнитного поля W выявил её выраженно нелинейный и немонотонный характер. Наблюдается резкое, более чем 40-кратное падение эффективности при росте энергии магнитного поля от 1.2 до 35.7 мкДж. Особенно показательно, что катушки с наименьшей энергией магнитного поля (1.2-3.7 мкДж) демонстрируют на порядок более высокую эффективность, чем катушки с максимальной энергией (35.5-35.7 мкДж). Это прямое экспериментальное подтверждение того, что энергия магнитного поля не является определяющим фактором эффективности процесса генерации ЭДС самоиндукции.
Вывод.
Проведённый анализ демонстрирует фундаментальное противоречие с классической трактовкой: если ЭДС самоиндукции не зависит от энергии магнитного поля, а энергия магнитного поля однозначно определяется энергией, переданной от источника питания, то неизбежно следует вывод о независимости процесса генерации ЭДС самоиндукции от самого источника питания.
Таким образом, экспериментально доказана полная энергетическая автономия процесса генерации ЭДС самоиндукции от традиционных источников энергии в системе.
Полученные результаты требуют пересмотра существующей физической модели явления самоиндукции. Взамен классического представления о прямой связи ЭДС самоиндукции с энергией магнитного поля необходима разработка новой теоретической платформы, учитывающей выявленную независимость этих параметров и объясняющей механизм стабилизации амплитуды ЭДС самоиндукции.
Критика классических представлений о самоиндукции на основе экспериментальных аномалий.
Опубликовано: 03/12/25
Проведённые эксперименты с переходными процессами в RL-цепи выявили ряд систематических аномалий,
которые в совокупности ставят под сомнение несколько фундаментальных постулатов классической
электродинамики.
Пространственно-временное разделение причины и следствия.
Классическая модель утверждает, что ЭДС самоиндукции Eₛ = –L (dI/dt) является мгновенной реакцией контура на изменение тока, стремящейся сохранить энергию магнитного поля. Однако эксперимент показывает: высоковольтный импульс ЭДС формируется строго после полного размыкания цепи, когда связь с источником питания и его ЭДС отсутствует. Процесс инициирован прошлым действием (изменением тока), но реализуется как самостоятельное энергетическое событие в уже разомкнутой системе.
Парадокс однополярных импульсов.
Ключевое наблюдение: импульсы ЭДС самоиндукции сохраняют однополярность независимо от изменения направления тока.
- При ключе в нижнем плече — импульсы положительные.
- При ключе в верхнем плече — импульсы отрицательные.
- При одновременном размыкании двух ключей (до и после катушки) формируются два независимых импульса противоположной полярности.
Данный факт необъясним в рамках модели Eₛ = –L (dI/dt), где знак ЭДС должен меняться с изменением знака dI/dt. Полярность импульса определяется не динамикой тока, а топологией точки разрыва цепи относительно «земли». Это указывает на то, что мы наблюдаем не «ЭДС индукции», а потенциальный выброс, чья природа коренится в структуре энергетического поля разомкнутой системы.
Энергия как первичная субстанция, а не следствие поля.
Эксперимент с ферритовым датчиком опровергает распространённый миф — что катушка «запасает энергию в магнитном поле», которое затем «выделяется».
- Датчик не фиксирует значительного магнитного поля перед импульсом.
- Мощное магнитное поле регистрируется строго одновременно с высоковольтным импульсом.
- Направление силовых линий указывает на их расхождение от центра катушки к полюсам, что противоречит общепринятым представлениям о структуре поля соленоида.
Это свидетельствует о том, что импульс ЭДС (потенциальная энергия) является причиной, а не следствием, наблюдаемого магнитного поля.
Наличие потенциальной энергии в несвязанном пространстве.
Осциллограф демонстрирует наличие разности потенциалов между электрически не связанными точками цепи (например, между точкой разрыва и «землёй» или даже щупом в воздухе). Это означает, что энергия, высвобождаемая при коммутации, проявляется не только как ток или напряжение в проводниках, но и как стационарное потенциальное поле в окружающем пространстве. Данный потенциал точно повторяет форму импульса, подтверждая, что источником возмущения пространства является именно энергетический импульс, а не ток в проводнике.
Заключение.
Совокупность этих фактов приводит к выводу, что классическое уравнение Eₛ = –L (dI/dt) описывает лишь корреляцию, но не раскрывает физическую суть процесса. Энергия, высвобождаемая при разрушении тока, ведёт себя как самостоятельная физическая субстанция. Она способна:
- существовать и преобразовываться после прекращения причинного тока;
- порождать однополярные потенциальные импульсы, природа которых зависит от топологии разрыва;
- создавать измеримые потенциалы в пространстве без гальванической связи;
- являться первичным источником для регистрируемых магнитных полей.
Таким образом, необходим переход от модели «ток → магнитное поле → ЭДС» к модели, где энергетический импульс (потенциальное поле) рассматривается как первичный агент, обуславливающий все последующие электромагнитные явления в переходном процессе. Эксперименты указывают на необходимость такой парадигмы.
Статьи, параметрический резонанс.
Опубликовано: 15/05/24
- Л.И. Мандельштам и Я.Д.Папалекси 1934г. Параметрическое возбуждение электрических колебаний.
- И.Греков Резонанс. 1952 год.
- Л.И.Мандельштам Лекции по колебаниям 1930-1932.
- The principle of the parametric power conversion.
- Simulation of a Parametric Oscillator Circuit, Part 1.
- Simulation of a Parametric Oscillator Circuit, Part 2.
- Parametric Excitation N.Minorsky
- Eric Dollard - Origin of Energy Synthesis.
- Video: Parametric Excitation of Electric Oscillations
- Video: Harmonic oscillation HD
- А.С.Сафонов - Основы электротехники - 1961
- Parametric Excitation of Electric Oscillations.
- Demonstration of Parametric Excitation.
Мищук Андрей.
Подборка.
- Что такое энергия электрического тока?
- Где конденсатор хранит заряд.
- Свободная энергия в колебательном контуре.
- Как увеличить энергию конденсатора.
- Индукционный нагреватель.
- Электронный уплотнитель мощности.
- Сверхтоки разряда конденсатора.
- Линейный ускоритель.
- Сагаер как преобразователь энергии.
- Резонанс в LTSpice.
- Язык программирования форт.